Hay \(n\) puntos en el plano. El \(i\)-ésimo punto tiene coordenadas \((x_i, y_i)\). Dispones de dos plataformas horizontales, cada una de longitud \(k\). Cada plataforma se puede colocar en cualquier parte del plano, pero debe ser horizontal (misma coordenada \(y\)) y tener bordes en enteros. Si el borde izquierdo de la plataforma está en \((x,y)\), entonces el borde derecho está en \((x + k,y)\), y todos los puntos entre esos bordes (incluyéndolos) pertenecerán a la plataforma.

Ten en cuenta que las plataformas pueden solaparse y no es necesario colocarlas a la misma coordenada \(y\).

Cuando colocas ambas plataformas, todos los puntos comienzan a caer (disminuyen su \(y\)). Si un punto colisiona con alguna plataforma en algún momento, se detiene y se salva. Los puntos que nunca colisionan con ninguna plataforma se pierden.

Tu tarea es encontrar el número máximo de puntos que puedes salvar colocando óptimamente las dos plataformas.

Entrada

La primera línea contiene un entero \(t\) \((1 ≤ t ≤ 2 * 10^4)\): el número de casos de prueba.

Cada caso de prueba se describe con tres líneas:

1. Una línea con dos enteros \(n\) y \(k\) \((1 ≤ n ≤ 2*10^5; 1 ≤ k ≤ 10^9)\): el número de puntos y la longitud de cada plataforma.
2. Una línea con \(n\) enteros \(x_1, x_2, …, x_n\) \((1 ≤ x_i ≤ 10^9)\): las coordenadas \(x\) de los puntos.
3. Una línea con \(n\) enteros \(y_1, y_2, …, y_n\) \((1 ≤ y_i ≤ 10^9)\): las coordenadas \(y\) de los puntos.

Se garantiza que todos los puntos son distintos y que la suma de \(n\) sobre todos los casos no excede \(2*10^5\).

Salida

Para cada caso de prueba, imprime un solo entero: el máximo número de puntos que puedes salvar.

Ejemplos

Nota

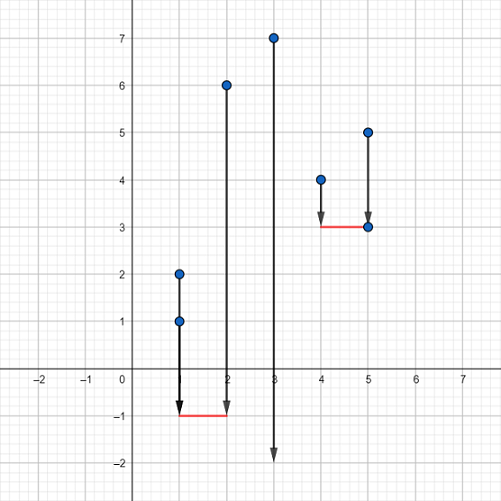
En el primer caso de prueba, una forma óptima es colocar:

• Una plataforma de longitud 1 entre \((1,–1)\) y \((2,–1)\).
• La otra plataforma de longitud 1 entre \((4,3)\) y \((5,3)\).

De este modo se salvan todos los puntos salvo \((3,7)\).